Keyword [DeepLabv1] [Dilated Conv] [CRF]
Chen L C, Papandreou G, Kokkinos I, et al. Semantic image segmentation with deep convolutional nets and fully connected crfs[J]. arXiv preprint arXiv:1412.7062, 2014.
1. Overview
In this paper, it proposes DeepLabv1 for segmentation.
- Dilated Conv.
- CRF.
- Multi-scale Prediction.
1.1. Details in Conv
1) Skip subsampling after the last two max-pooling layers of VGG16.
2) Exploit Dilated Conv.
3) Reduce $7 \times 7$ Conv to $4 \times 4$ or $3 \times 3$ for saving computation time.
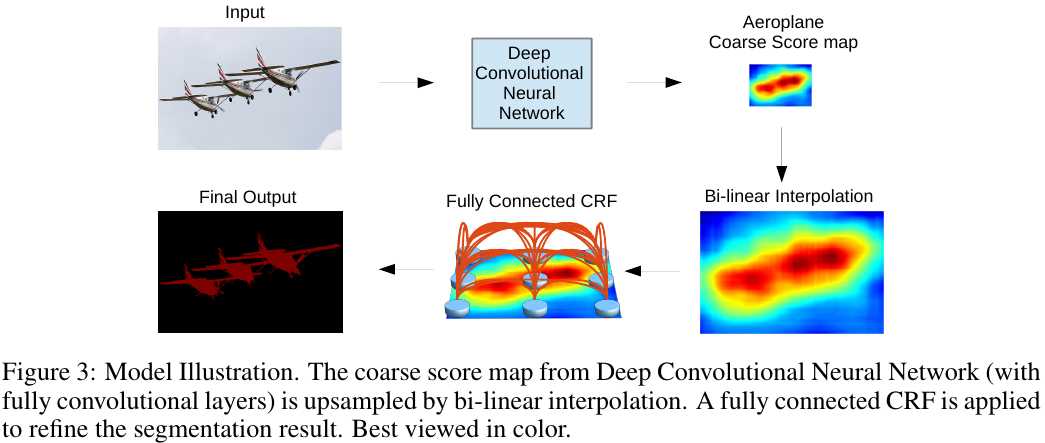
1.2. Conditional Random Fileds

Energy Function: $E(x) = \sum_i \theta_i (x_i) + \sum_{ij} \theta_{ij}(x_i, x_j)$.
1) x. label assignment for pixels.
2) $\theta_i (x_i) = -\log P(x_i)$. [$P(x_i)$ is the label assignment probability at pixel $i$].
3) $\theta_{ij}(x_i, x_j)=\mu (x_i, x_j) \sum_{m=1}^{K} w_m \cdot k^m (f_i, f_j)$. [$\mu (x_i, x_j)=1$ if $x_i \ne x_j$ ]
4) $k^m$ is the Gaussian kernel depends on feature of pixel $i,j$, weighted by $w_m$:
$w_1 \exp (-\frac{|| p_i - p_j ||^2}{2 \sigma_{\alpha}^2} - \frac{|| I_i - I_j ||^2}{2\sigma_{\beta}^2}) + w_2 \exp (- \frac{|| p_i - p_j ||^2}{2\sigma_{\gamma}^2})$
5) The first kernel depends on both pixel positions ($p$) and pixel color intensities ($I$). The second kernel only depends on pixel positions. The hyper parameter $\sigma_x$ controls the scale of the Gaussian kernels.